中学趣味数学:浅谈城镇经济发展与水资源的合理利用

概要：=（11.2－2x）×升；总需水量=2.4×升+x·升+（11.2-2x）×升=（13.6十8x）·升．∵m=·V（），∴总需水量=(13.6+8x）·吨．若想满足使用需要，则总用水量≤总出水量．∵总用水量随x的增加而增大（单位面积每日的需水量工业最大），∴x的最大值决定于总出水量的最大值（前提：总出水量≤地下水得到的补给量）若想提高总出水量，有2种方法：（1）改用大功率的抽水机，提高单口井的出水量．本方法肯定会使井所在的局部地区地下水人不敷出，致使地下水位下降，甚至引起局部塌陷等严重后果．而无井地区的地下水资源却还很丰富．（2）多建并本方法可以使井的分布更加均匀合理，最大限度开发地下水资源．∴应选择方法（2），且每口井的日出水量不大于360吨，否则会出现方法（1）导致的后果．那么，究竟该建几口井，怎么建呢？首先，井的位置应均匀分布在辖区内．其次，关于井的数量．根据北京市现行的规划指标，井的分布密度最高为每200亩一口井．

中学趣味数学:浅谈城镇经济发展与水资源的合理利用,标签：七年级数学练习题,http://www.kgf8.com
=（11.2－2x）×升；

　　总需水量=2.4×升+x·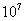升+（11.2-2x）×升=（13.6十8x）·升．

　　∵m=·V（），

　　∴总需水量=(13.6+8x）·吨．　

　　若想满足使用需要，则总用水量≤总出水量．

　　∵总用水量随x的增加而增大（单位面积每日的需水量工业最大），

　　∴x的最大值决定于总出水量的最大值（前提：总出水量≤地下水得到的补给量）若想提高总出水量，有2种方法：　　（1）改用大功率的抽水机，提高单口井的出水量．

　　本方法肯定会使井所在的局部地区地下水人不敷出，致使地下水位下降，甚至引起局部塌陷等严重后果．而无井地区的地下水资源却还很丰富．

　　（2）多建并

　　本方法可以使井的分布更加均匀合理，最大限度开发地下水资源．

　　∴应选择方法（2），且每口井的日出水量不大于360吨，否则会出现方法（1）导致的后果．

　　那么，究竟该建几口井，怎么建呢？

　　首先，井的位置应均匀分布在辖区内．

　　其次，关于井的数量．根据北京市现行的规划指标，井的分布密度最高为每200亩一口井．否则分布过密，相邻两口井它们在地下抽的水却是一个区域的，这样既使每口井的日出水量都不大于360吨，也会出现方法（1）导致的后果．

　　∵井数=（l亩≈666，马坊镇中心区现有20口井），

　　∴总出水量max=360吨×45=16200吨．

　　∵总需水量≤总出水量，

　　∴最大需水量（13.6+8x）×10³=16200（吨）．于是x=0.325．

　　五、结果　　

　　在不破坏自然生态的前提下，平谷县马坊镇镇中心区最多可以建设0.325平方千米的工业区．

　　六、误差分析及几席说明　　

　　1．本次讨论所应用的数据均为规划资料，与马坊镇中心区的实际情况之间会有些出人．

　　2．对于农田的用水本次讨论取了每天的平均值，然而农业生产实际的需水量与季节有关，并非每日都一样．　　

　　3．由于实际需要，每口井均24小时不间断的出水而生活、农业、工业的用水日间与夜间的差异却很大，为弥补这个用水量在时间上的变化的缺陷，建议多建设一些营水工程，把夜间抽出的水蓄起来以备日间使用，并把一些对时间要求不大的工厂改在夜间进行生产．

　　4．建井的位置与地下水资源的分布，地形的高低等有关，实际建设中不一定必须按200亩一口的标准建设，且建设还受资金条件的影响．

　　5．以上结果为理论值，与实际应用会有偏差．

上一页  [1] [2] 

　 上一篇：中学趣味数学:科拉致死